 →
→
Tillbaka till Hans Lundmarks startsida
Vi värmer upp med lite lätt stretching (av Brian Edgar). Avbildningsmatrisen är
[ 1 1/2 ]
A = [ ] .
[ 0 1 ]
 →
→

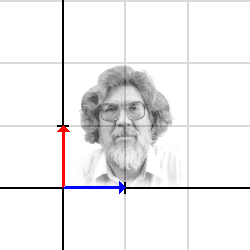
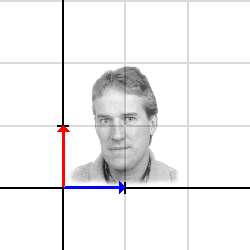
Standardbasvektorerna
[ 1 ] [ 0 ] [ ] , [ ] [ 0 ] [ 1 ]
är markerade med blått resp. rött i den första bilden.
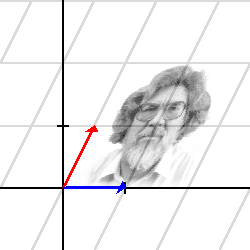
Matrisens kolonner
[ 1 ] [ 1/2 ] [ ] , [ ] [ 0 ] [ 1 ]
anger basvektorernas bilder. (Blått resp. rött i den andra bilden.)
Dessa bestämmer i sin tur hela avbildningen på grund av lineariteten, vilket illustreras av rutnäten. Rutorna har samma area i båda rutnäten, vilket stämmer med att determinanten (avbildningens areaskala) är 1.
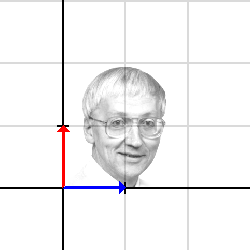
Nu är det Arne Enqvists tur. Vi utsätter honom för en symmetrisk avbildning:
[ 1 1/2 ]
A = [ ] .
[ 1/2 1 ]
Determinanten är 3/4, så rutornas (och Arnes) area minskar lite.
 →
→
Det ska finnas en ON-bas av egenvektorer enligt spektralsatsen, eftersom avbildningen är symmetrisk. Mycket riktigt: med den vanliga beräkningen (eller med kvalificerad gissning) finner vi
[ 1 1/2 ] [ 1 ] 3 [ 1 ] [ ] [ ] = - [ ] , [ 1/2 1 ] [ 1 ] 2 [ 1 ] [ 1 1/2 ] [ -1 ] 1 [ -1 ] [ ] [ ] = - [ ] . [ 1/2 1 ] [ 1 ] 2 [ 1 ]
Normerade egenvektorer är alltså
1 [ 1 ] 1 [ -1 ] ------- [ ] , ------- [ ] sqrt(2) [ 1 ] sqrt(2) [ 1 ]
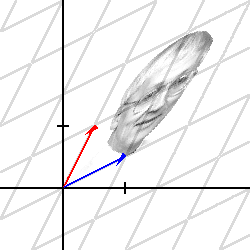
vilka vi tar som nya basvektorer. Vi tittar på samma avbildning igen, men i koordinatsystemet som ges av denna nya bas. Luta huvudet 45 grader åt vänster, och försök att glömma det gamla koordinatsystemet helt och hållet!
 →
→
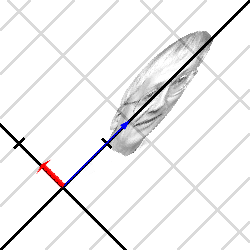
Nu ser man tydligt varför areaskalan är 3/4: avbildningen sträcker (3/2) i en riktning och trycker ihop (1/2) i den ortogonala riktningen. Den första (blå) egenvektorn, som nu – kom ihåg vi har bytt koordinatsystem! – har koordinaterna
[ 1 ] [ ] , [ 0 ]
avbildas på
[ 3/2 ] [ ] , [ 0 ]
medan den röda avbildas på
[ 0 ] [ ] . [ 1/2 ]
Detta ger oss kolonnerna i den nya avbildningsmatrisen D (som beskriver samma avbildning, fast i det nya koordinatsystemet):
[ 3/2 0 ]
D = [ ] .
[ 0 1/2 ]
Matrisen blir alltså helt enkelt diagonal, med egenvärdena på diagonalen. Determinanten är produkten av egenvärdena. "Byt bas och se bättre!", som Peter Hackmans berömda sång säger.
Thomas Karlsson vill nog också vara med. En spegling får det bli för hans del:
[ 5/13 12/13 ]
A = [ ] .
[ 12/13 -5/13 ]
Till skillnad från de tidigare exemplen så är determinanten här negativ (−1 för att vara exakt), så orienteringen ändras. Mycket riktigt så är Thomas spegelvänd i den andra bilden, vilket du ser om du vrider på huvudet och tittar efter.
 →
→
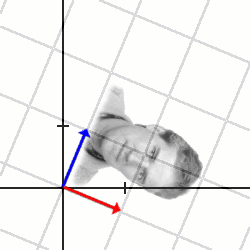
Övning 1: Var är speglingslinjen?
Övning 2: Den här avbildningen är också symmetrisk. Hitta en ON-bas av egenvektorer. Vad blir avbildningsmatrisen i denna nya bas?
[an error occurred while processing this directive] Ursprunglig version 2000-10-08. Senast ändrad 2022-08-05. Hans Lundmark (hans.lundmark@liu.se)