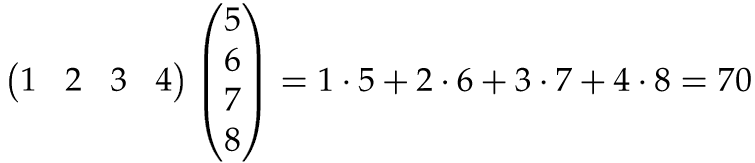
Back to Hans Lundmark's main page
Matrix multiplication is a very useful operation in mathematics, although the definition may seem a bit difficult and unnatural when first encountered. Here I won't go into why it is so useful. I will merely give a quick description of how to do it, illustrating with a few examples.
This document is supposed to be slightly interactive, which only works if you have JavaScript enabled in your web browser. Try moving your mouse pointer over the formulas and watch what happens!
First, here is how to multiply a row matrix with a column matrix of the same length – that is, with the same number of entries. The result is a number (which can be viewed as a 1x1 matrix if one insists that the product of two matrices always must be a matrix).
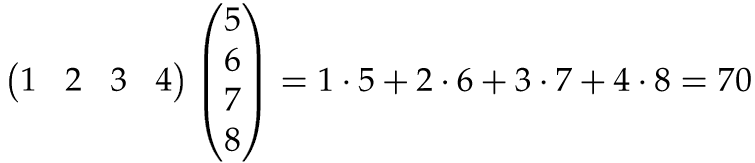
In this example, the row and the column both have length 4, but the same pattern obviously works whenever they are of the same length; just multiply corresponding entries and sum up. If the row and the column are not of the same length, their product is undefined.
And now two general matrices, A and B, say. The matrix product AB is formed by multiplying every row of A with every column of B, in the way described in Step 1 above. The resulting numbers are arranged in a new matrix: the mth row in A times the nth column in B gives the number at position (m,n) in AB:
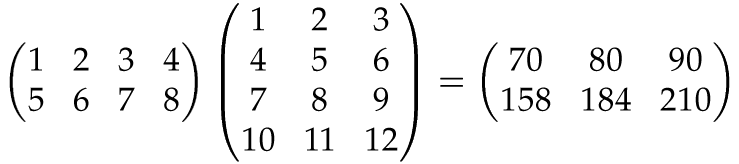
Again, for this to work, the rows of A must have the same length as the columns of B. If not, the product AB is undefined:
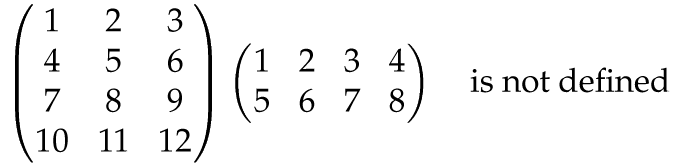
So even if AB is defined, BA need not be defined. And even when AB and BA are both defined, they are usually not equal.
That's all, folks! Much more can be said about matrix multiplication, but that won't fit into a micro-course like this. Maybe if I get the inspiration, I'll expand this into a mini-course someday...
Original version 2001-01-23. Last modified 2019-11-29. Hans Lundmark (hans.lundmark@liu.se)