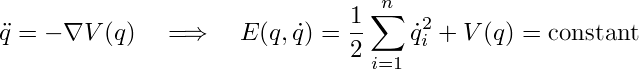
Back to Hans Lundmark's main page
An important class of systems in classical mechanics are those of Newton type: d2q / dt2 = M(q), where q = (q1,…,qn) is a point in Rn. Equation of this form are obtained from Newton's second law (acceleration equals force divided by mass) if the force field depends only on positions and not on velocities.
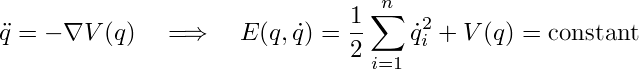
Newton systems appearing in physics often take the form d2q / dt2 = −∇V(q) for some scalar function V(q) called the potential. This reflects the conservation of the energy (kinetic + potential); in mathematical terms, E = T + V = (1/2) ∑ (dqi / dt)2 + V(q) is a constant of motion for the system. There is a lot of mathematical machinery for dealing with such systems: Lagrangian mechanics, Hamiltonian mechanics, etc.
In order to have any hope of integrating the system (that is, computing the solution explicitly), one must find sufficiently many other constants of motion besides the energy. Such extra constants of motion may or may not exist, depending on what the potential V is.
For those rare systems where it is possible to perform the integration explicitly, this is often accomplished through the powerful Hamilton–Jacobi method, which uses separation of variables in a clever way in order to compute the solution. A potential for which this method is applicable is called a separable potential. (There is a remarkable algorithm, due to Stefan Rauch-Wojciechowski and Claes Waksjö, for determining whether a given potential is separable or not.)
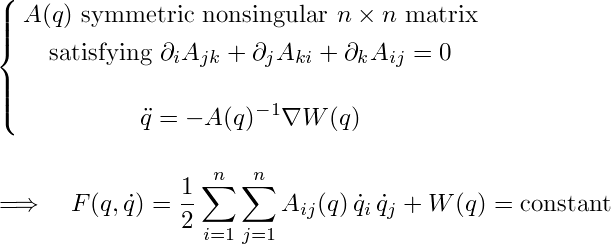
Quasi-potential systems are more general; they are Newton systems having a constant of motion which is energy-like in the sense that it depends quadratically on the the velocity components: F = (1/2) ∑∑ Aij(q) (dqi / dt) (dqj / dt) + W(q). (Such constants of motions appear besides E for systems given by a separable potential, but here we are not assuming that the system has a potential at all.)
By simply computing dF/dt and setting it to zero, one finds that the right-hand side M of such a Newton system (written as a column vector) must be given by M(q) = −A(q)−1∇W(q) for some scalar function W(q), called the quasi-potential, and some n×n symmetric matrix function A(q) satisfying the condition ∂i Ajk + ∂j Aki + ∂k Aij = 0 for all indices i,j,k = 1,…,n. (Such a matrix is called a Killing tensor for the Euclidean metric.)
When I started out as a PhD student, my first project was to study quasi-potential systems in two dimensions together with Stefan Rauch-Wojciechowski and Krzysztof Marciniak.
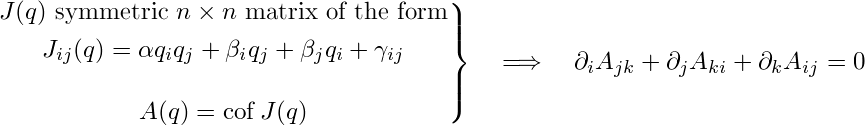
Later, when I tried to generalize our results to n dimensions, it turned out that one has to restrict the class of quasi-potential systems a bit in order for the theory to work.
A cofactor system is a quasi-potential system where the matrix A(q) has the following special form: A(q) = cof J(q), where Jij(q) = αqiqj + βiqj + βjqi+γij. Here, "cof" denotes taking the cofactor matrix (defined by the formula X cof X = (det X)I ; also called the adjoint matrix), and α, βi and γij = γji are real parameters. The corresponding quadratic constant of motion F is said to be of cofactor type.
(Notice that if n > 2, then A(q) depends on the parameters α, βi, γij in a fairly complicated way, so the set of matrices of the form A(q) = cof J(q) is a nonlinear variety in the (linear) solution space to ∂i Ajk + ∂j Aki + ∂k Aij = 0. When n = 2, these matrices fill out the whole solution space.)
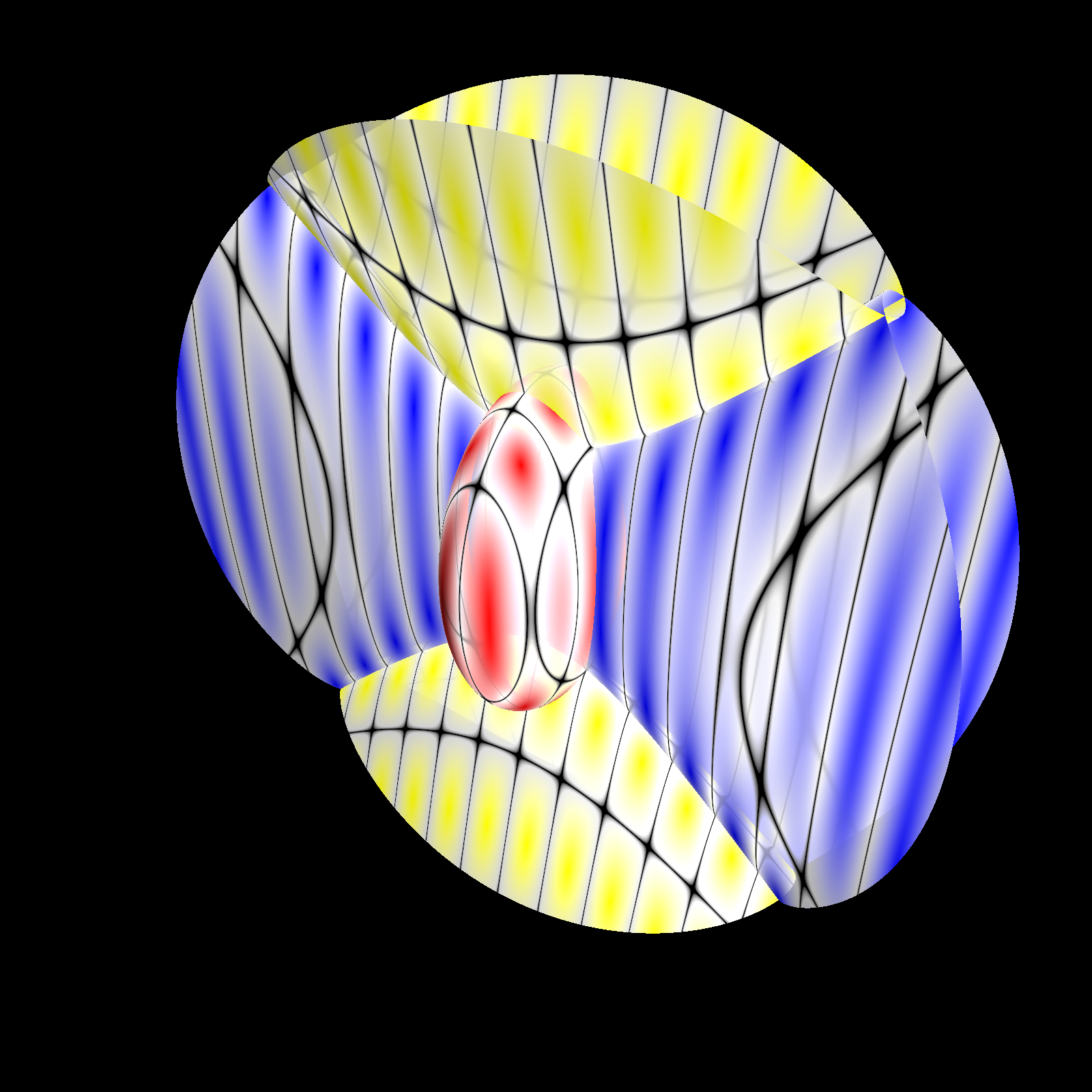
I called matrices J(q) of this particular type elliptic coordinates matrices because of their relation to Jacobi's generalized elliptic coordinates: in fact, the eigenvalues u1,…,un of such a matrix are functions of q, and this relationship u = u(q) is precisely the change of variables from Cartesian coordinates (q1,…,qn) to elliptic coordinates (u1,…,un). (In three dimensions, the level surfaces of elliptic coordinates are ellipsoids, one-sheeted hyperboloids, and two-sheeted hyperboloids, intersecting at right angles as illustrated below.)

As I learned later, such matrices J(q) had appeared earlier in the literature under various names; for example, Sergio Benenti had referred to a special case as inertia tensors. Mike Crampin and Willy Sarlet (who generalized the concept of cofactor systems from Euclidean space to Riemannian manifolds) called them special conformal Killing (SCK) tensors, which is the name that seems to be most used nowadays.
Some of the classical machinery for potential systems can still be used for cofactor systems. In particular (although I will not try to explain here exactly what it means), a cofactor system can be embedded in a (2n+1)-dimensional phase space in such a way that it is Hamiltonian with respect to a certain noncanonical Poisson structure which depends on the parameters appearing in the matrix J(q). Maciej Błaszak and Krzysztof Marciniak have shown that cofactor systems are essentially potential systems up to reparametrization of time. Work in progress by Alain Albouy and me shows that cofactor systems are precisely those Newton systems which admit a potential "in the sense of projective dynamics".
A bi-cofactor system (or a cofactor pair system) is a system which can be written as a cofactor system in two independent ways. Thus, by definition, a bi-cofactor system is a system which has two independent constants of motion of cofactor type, with SCK tensors J1 and J2, respectively.

It is a remarkable and quite nontrivial fact that a bi-cofactor system automatically has n quadratic constants of motion! My original proof of this used that each of the two cofactor-type constants of motion gives rise to a Poisson structure, so that the system is bi-Hamiltionan. Crampin and Sarlet gave a more direct proof which is very elegant, but uses a bit of machinery about differential operators of a certain kind ("Frölicher–Nijenhuis derivations of type d*"). Yet another proof comes out of the "projective dynamics" view of cofactor systems.
There is a simple recipe (which I skip here) for finding the n−2 extra constants of motion from the two given ones. Provided that all these constants of motion are functionally independent, the system can be considered as completely integrable in the Liouville–Arnold sense. In particular, when one of the two given constants of motion is the usual energy E, the system is given by a separable potential, and this theorem explains a lot of the structure of the constants of motion for such a system.
Now suppose that that we have two cofactor pair systems, both associated to the same pair (J1, J2) of SCK tensors. The multiplication theorem gives a formula for producing a third cofactor system associated to (J1, J2). Briefly, it works like this: for each of the two systems, compute the full set of n constants of motion (as guaranteed by the "2 implies n" theorem), and put the n quasipotentials as coefficients in a polynomial of degree n−1 in a parameter μ. Then multiply the two polynomials, and reduce modulo the degree n polynomial det(J1 + μ J2). The resulting polynomial contains the quasipotentials for the resulting "product" system.
A special case of this formula, when J1 = [1,0; 0,−1] and J2 = [0,1; 1,0], corresponds to the fact that the product of two holomorphic functions is again holomorphic. (The quasipotentials in this case are the real and imaginary parts of the holomorphic functions.) Another way of saying this is that there is a multiplicative structure on the solution set of the Cauchy–Riemann equations. Jens Jonasson has developed this point of view further, and studied linear systems of PDE with a similar multiplicative structure on their solution set.
Starting from the trivial system d2q / dt2 = 0, which is a bi-cofactor system with constant quasipotentials for any pair of SCK tensors, and taking "powers" with respect to this multiplication, one can produce infinite sequences of nontrivial bi-cofactor systems.
Last modified 2019-12-25. Hans Lundmark (hans.lundmark@liu.se)