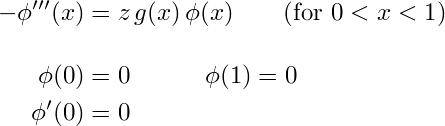
Back to Hans Lundmark's main page
The cubic string is the following eigenvalue problem, which plays an important role when deriving the explicit formulas for the multipeakon solution of the Degasperis–Procesi equation:
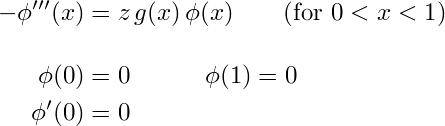
The function g(x) is given, and we seek the values of the parameter z (eigenvalues) for which the differential equation has solutions (eigenfunctions) satisfying the boundary conditions.
It is a third order problem, and not selfadjoint, but still it has some properties in common with the ordinary string problem described below. For example, if g is positive, then the eigenvalues are positive (and, in particular, they are real, which is not obvious).
To understand where the name "cubic string" comes from, consider the linear wave equation which describes small vibrations of an ordinary string (like a guitar string) fixed at the endpoints: g(x) utt = uxx, with boundary conditions u(0,t) = u(1,t) = 0. Here the function g(x) is the mass density per unit length of string, divided by the tension. Seeking a separated solution u(x,t) = φ(x) T(t) one finds that φ′′(x) / φ(x) g(x) = T′′(t) / T(t), which must be independent of both x and t, and therefore equal to some constant, say −z. This gives the (ordinary) string eigenvalue problem for the x-dependent part of the solution:
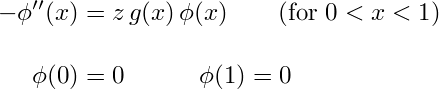
As you can see, the cubic string differs from this ordinary string only in having a third derivative instead of a second derivative, and having an extra boundary condition. (For a third order differential equations, three is the right number of boundary conditions.)
The ordinary string is a very classical problem in mathematical physics. It is selfadjoint, so the eigenvalues are automatically real. General solutions can be constructed as Fourier series of eigenfunctions.
A slightly degenerate, but very interesting, special case is the discrete string consisting only of a finite number of point masses connected by weightless string. To describe this mathematically, we must let g be a discrete measure (a linear combination of Dirac delta distributions) rather than a function. Then the equation says that φ′′ = 0 between the point masses, which means that the eigenfunctions are piecewise linear in x. In this case, the problem can be written as an eigenvalue problem for an n×n symmetric matrix, where n is the number of point masses, so there will be exactly n eigenvalues.
The discrete string plays an important role when deriving the multipeakon solution formulas for the Camassa–Holm shallow water equation (which was done by Richard Beals, David Sattinger and Jacek Szmigielski), and also for solving some other integrable systems like one of the variants of the Toda lattice (as first noticed by the great mathematician Jürgen Moser). Here it is actually the inverse eigenvalue problem which is most important; if we know the eigenvalues and a little bit of information about each eigenfunction (namely the ratio between the slopes at the left and right endpoints), how do we recover the mass distribution g? This is connected to a whole world of fascinating classical mathematics, like orthogonal polynomials, continued fractions of Stieltjes type, and Padé approximation, and from there to some things that are fashionable nowadays like random matrices.
For finding peakon solution of the Degasperis–Procesi equation, it is the discrete version of the cubic string which is of interest. Here, even the forward spectral problem poses a challenge, since it is not selfadjoint. How can we prove that the eigenvalues are real and simple, for example? It turns out that this can be handled using the theory of "oscillatory kernels" developed by F. R. Gantmacher and M. G. Krein. The inverse eigenvalue problem can be explicitly solved in the discrete case, and this has connections to generalizations of the classical stuff mentioned above, like "biorthogonal polynomials" for example. Marco Bertola, Michael Gekhtman and Jacek Szmigielski have written a series of papers where they investigate this more deeply. It turns out that there are random matrix models associated to the cubic string as well.
Last modified 2019-12-25. Hans Lundmark (hans.lundmark@liu.se)