Papers
1959
1960
1961
1962
1963
1964
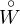 22 of the Dirichlet problem for a region with a smooth irregular
boundary. (Russian) Vestnik Leningrad. Univ. 19:7 163–165.
22 of the Dirichlet problem for a region with a smooth irregular
boundary. (Russian) Vestnik Leningrad. Univ. 19:7 163–165.
1965
1966
1967
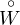 22 of the Dirichlet problem in a region with a smooth irregular boundary.
(Russian) Vestnik Leningrad. Univ. 22:7, 87–95.
22 of the Dirichlet problem in a region with a smooth irregular boundary.
(Russian) Vestnik Leningrad. Univ. 22:7, 87–95.
1968
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
1980
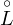 pl(Ω) into a space of generalized functions.
(Russian) Theory of analytic functions and harmonic analysis. Akad. Nauk Gruzin. SSR Trudy Tbiliss.
Mat. Inst. Razmadze 66, 70–83.
pl(Ω) into a space of generalized functions.
(Russian) Theory of analytic functions and harmonic analysis. Akad. Nauk Gruzin. SSR Trudy Tbiliss.
Mat. Inst. Razmadze 66, 70–83.
1981
1982
 sek, 1982), pp. 150–190, Teubner-Texte zur Math.
49, Teubner, Leipzig.
sek, 1982), pp. 150–190, Teubner-Texte zur Math.
49, Teubner, Leipzig.
1983
1984
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
2017
2018
2019
Books edited