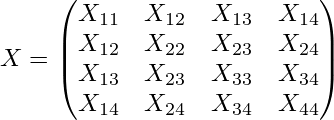
Back to Hans Lundmark's main page
The Canada Day Theorem is a curious combinatorial identity that unexpectedly cropped up when Andy Hone, Jacek Szmigielski and I were studying so-called peakon solutions to a nonlinear integrable PDE found by Vladimir Novikov in 2008.
For the story of how the theorem got its name, and also a description of our proof, see the slides from one of my talks. The result was first published in the appendix of our paper about Novikov peakons, and later with an improved proof in a separate paper.
The theorem deals with n×n matrices, where n is a fixed number. For the illustrations, I'll take n = 4.
Let X denote an arbitrary symmetric n×n matrix:
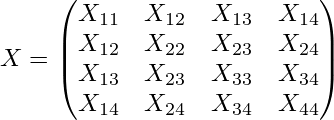
Let T be the n×n matrix with Tij equal to 0, 1, or 2, depending on whether i is less than, equal to, or greater than j:
If I and J are two index sets, each containing k of the numbers from 1 to n, then for any matrix A we let AI,J denote the k×k submatrix of A formed by the entries lying in the rows indexed by I and the columns indexed by J. For example,
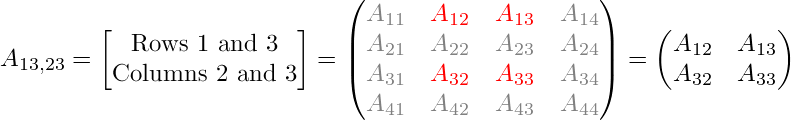
The determinant det(AI,J) of such a submatrix, is called a k×k minor of A. Those minors for which I = J are called the principal minors of A.
(As you may know, the coefficient of λn−k in the characteristic polynomial det(A − λI ) equals (up to sign) the sum of the k×k principal minors of A.)
For any k = 1, …, n, the sum of the principal k×k minors of the matrix TX equals the sum of all k×k minors of X.
Note that it's essential that X is symmetric, otherwise the theorem would not be true.
Let's look at the case n = 3, where the following 3×3 matrices are involved:
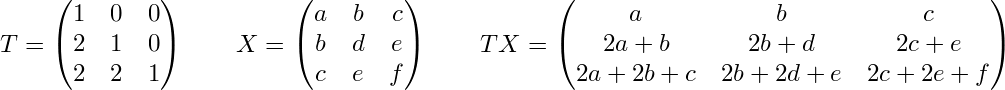
There are three possible values of k:
k = 1. The 1×1 minors of X are simply the entries of X, and their sum is a + d + f + 2b + 2c + 2e. On the other hand, the principal 1×1 minors of TX are the diagonal entries of TX, and their sum is a + (2b + d) + (2c + 2e + f), which is the same thing (as it should be, according to the theorem).
k = 3. There is only one 3×3 minor in a 3×3 matrix, namely the determinant of the whole matrix (and this is a principal minor). Thus, what the Canada Day Theorem states in this case is that the equality det X = det TX should hold. And this is indeed true, because of the law det TX = det T det X and the fact that det T = 1.
k = 2. This is more interesting. Now we are comparing two sums of 2×2 minors, as shown below. (The formulas are meant to indicate the 2×2 determinants formed by the red entries only; the grey entries are merely shown to make it easier to see where each minor sits inside the original matrix.)
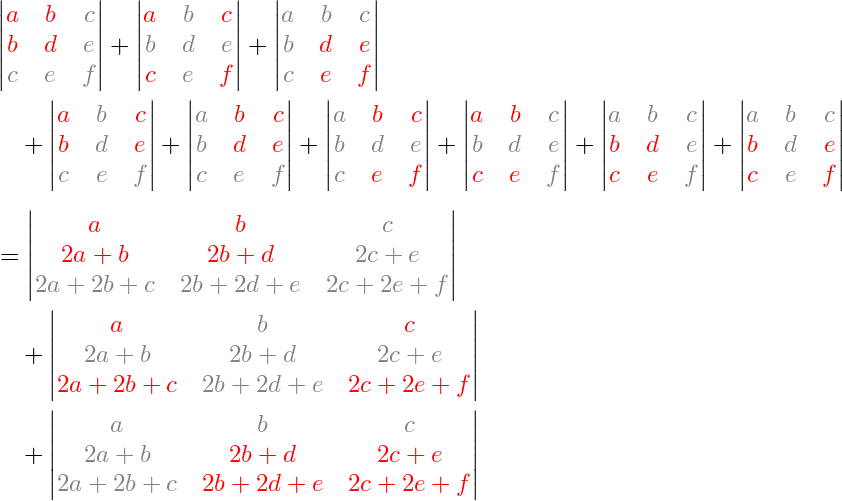
It's straightforward to verify that this is true as well.
You may have noticed in the big equation above (n = 3, k = 2) that it's possible to group the terms on the left-hand side so that each group of terms equals a corresponding determinant on the right-hand side. It's not that simple for n ≥ 4, as you may convince yourself by looking at some larger examples.
If (like me) you can't resist a little combinatorial challenge, then you might find it an interesting exercise to try to prove the theorem yourself. Please let me know if you find a really simple solution (or if you've seen this result somewhere else in the literature)!
Last modified 2019-12-25. Hans Lundmark (hans.lundmark@liu.se)