Back to Hans Lundmark's main page
The Degasperis–Procesi equation (or DP equation) is the following nonlinear integrable PDE, which was found in 1998 by Antonio Degasperis and Michela Procesi:
Here u(x,t) is the unknown function that we seek, and the subscripts denote partial derivatives.
We can use the abbreviation m = u−uxx to write the DP equation on the simpler form mt+mxu+3mux = 0. Like its more famous cousin, the Camassa–Holm shallow water equation mt+mxu+2mux = 0 derived in 1993 by Darryl Holm and Roberto Camassa, the DP equation admits an interesting class of solutions called peakons (peaked solitons).
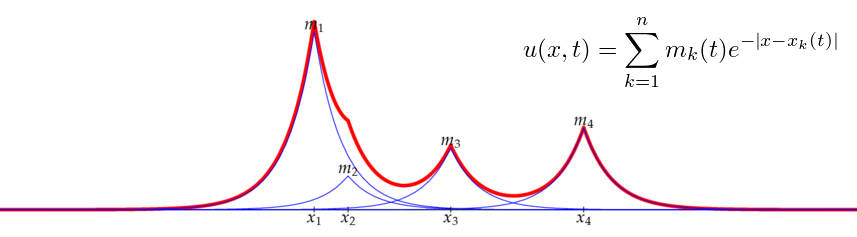
The n-peakon solution is a superposition of n interacting peak-shaped waves, each with its own time-dependent position xk(t) and amplitude mk(t):

Solutions of this form must be interpreted in a suitable weak sense, since they are not differentiable at the points xk.
Below is a movie showing one particular four-peakon solution of the DP equation. (A larger version of the movie is also available, which is annotated like the figure above and runs a little slower so that it's easier to follow what's going on: 6 MB GIF animation.)

As you can see, a peakon moves faster the taller it is, and when a fast peakon catches up with a slow one, it "gives it a push"; the faster one slows down and the slower one speeds up, like sprinters exchanging the baton in a relay race.
The time dependence of the positions and amplitudes is governed by a system of 2n ordinary differential equations, which looks different for different peakon PDEs. In shorthand notation, the system for the DP equation is
Jacek Szmigielski and I managed to derive explicit formulas for the general solution of these Degasperis–Procesi peakon ODEs for any n. (After two years of hard work! Jacek had previously solved the corresponding ODEs for Camassa–Holm peakons together with Richard Beals and David Sattinger, and the DP case was supposed to be my "warm-up problem" when I came to Saskatoon for my postdoc in 2002. However, it turned out to be a liiittle bit more difficult than expected. Our joint paper which describes the whole procedure is 64 pages long.)
Below, you can see in detail what the system and the solution formulas look like in the case n = 4 (assuming that we number the peakons so that x1 < x2 < x3 < x4). From this, you will probably be able to guess what the pattern is for arbitrary n.
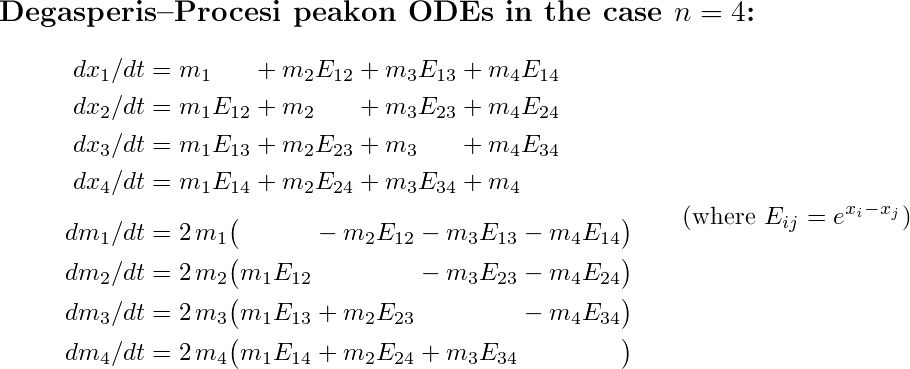

Last modified 2019-12-25. Hans Lundmark (hans.lundmark@liu.se)