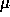(avrundningsenheten i flyttalssystemet). Antag, att man ska
implementera standardfunktionen
Då man implementerar standardfunktioner på en dator bör man
kräva att de ger full noggrannhet, att alla bitarna i taldelen är
korrekta, dvs att det relativa felet är mindre än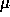
(avrundningsenheten i flyttalssystemet). Antag, att man ska
implementera standardfunktionen
på en dator i IEEE enkel precision. Antag vidare att man har en
implementation av exponentialfunktionen, som ger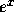 
med relativt fel
mindre än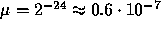 
för alla
x sådana att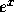 
kan representeras i flyttalsformatet. För
stora x går det bra att
använda definitionen (1), men för små x uppstår
kancellation. Låt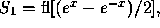 
beteckna resultatet då standardfunktionen 
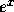används och
subtraktionen utförs i flyttalssystemet. Följande värden erhölls på en
SUN arbetsstation (Fortran-kod):
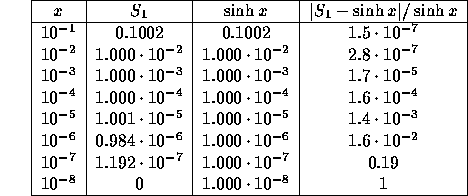
Om man i stället använder de tre första termerna i MacLaurin-utvecklingen
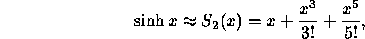
så får man på arbetsstationen felet 0 (vilket inte
betyder att felet är lika med noll utan att skillnaden mellan den
``inbyggda'' standardfunktionen och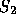 
är lika med noll).
Vi ska nu visa att det relativa felet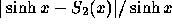 
är
tillräckligt litet för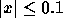 
. Vi har
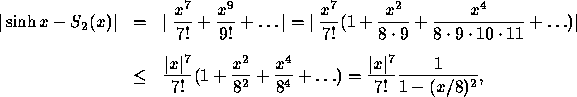
där vi har summerat en geometrisk serie.
Eftersom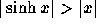 
, kan vi uppskatta det relativa felet
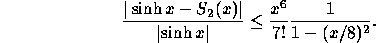
Det största felet får vi för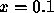 
:
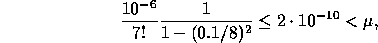
vilket visar att approximationen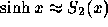 
är
tillräckligt noggrann.
Om man beräknar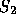 
i utökat flyttalsformat (se Avsnitt 2.8 i
boken) så blir avrundningen till enkel precision det dominerande
felet och man får full noggrannhet (relativt fel mindre än
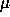) i approximationen av 
.
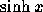This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds. The command line arguments were:
latex2html -split 0 sinhypexempel.tex. The translation was initiated by Lars Elde'n on Mon Nov 27 16:40:15 MET 1995
