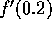Numerisk derivering - Richardsonextrapolation

Beräkna 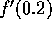så noggrannt som möjligt då f ges av följande korrekt avrundade tabell.

Använd centraldifferens (Kap. 6.2)

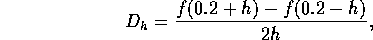
och upprepad Richardsonextrapolation (Kap. 6.4).

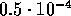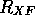Eftersom de absoluta felen i funktionsvärdena är mindre än kan i 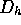-värdena uppskattas (Kap. 6.3)

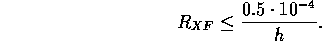
Algoritm:

repeat

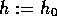
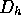Beräkna och Richardsonextrapolera

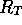Uppskatta och

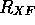
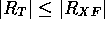if then STOP else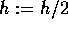

Vi beräknar differensapproximationer för steglängderna 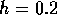och 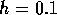, och gör en Richardsonextrapolation. Samtidigt gör vi ett störningsschema för :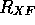

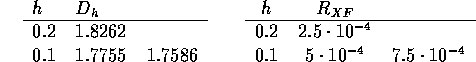
Ur Richardsonschemat ser vi att 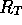kan uppskattas (Kap 6.4)

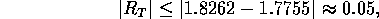
vilket är mycket större än 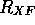, så vi måste halvera steglängden och beräkna en ny differensapproximation, samt extrapolera:

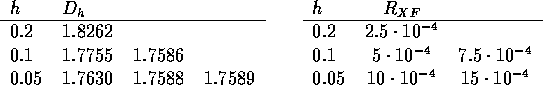
Vi uppskattar

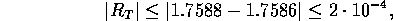
vilket är mindre än 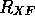för värdena i extrapolationsschemat.

Totalt fel:

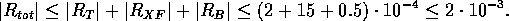
(Vi har räknat med större noggrannhet och avrundat till fyra decimaler. Därför ).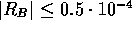

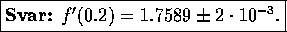
About this document ...

This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds. The command line arguments were: latex2html -split 0 der_rich_ex.tex. The translation was initiated by Lars Elde'n on Mon Nov 27 16:32:10 MET 1995