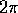Approximation

Brusreducering med Fourier-analys

Antag att vi har mätt upp en periodisk signal (med perioden 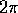), som innehåller ett antal sinuskomponenter plus brus:

Antag vidare (för enkelhets skull) att vi vet att summan har 8 sinuskomponenter. Vi har modellen

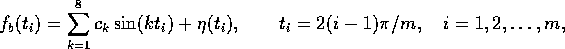
där 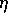är bruset och vi har samplat signalen vid m=100 tidpunkter .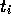

Vi ska uppskatta koefficienterna 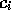med minsta kvadratmetoden och samtidigt reducera bruset. Med beteckningarna från Kapitel 9 i boken har vi

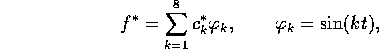
där koeeficienterna 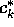fås ur normalekvationerna.

Vi har skalärprodukten

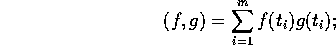
man kan visa, att vi har

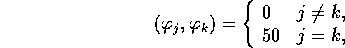
dvs funktionerna 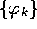är ortogonala. Lösningen till normalekvationerna blir därför helt enkelt

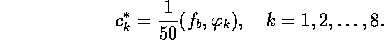
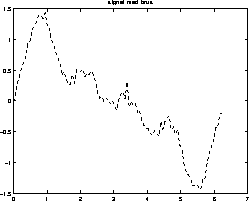
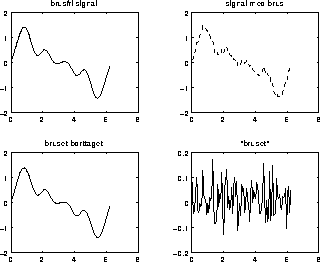
I nedanstående figur har vi illustrerat den ``rätta'' signalen utan brus, signalen med brus (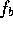), signalen med bruset borttaget (minsta kvadratlösningen 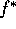), och ``bruset'' (residualen ).

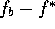Beräkningarna blir mycket enkla i Matlab:

m=100; h=2*pi/m; t=0:h:2*pi-h/2; % Vector of t(i) values 

for k=1:8,
  phik=sin(k*t)';             
  xc(k)=(2/m)*(phik'*fb);        % Solution of normal equations
end

I realistiska tillämpningar utförs beräkningarna med snabb Fourier-transform (FFT).

About this document ...

This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds. The command line arguments were: latex2html -split 0 fourier.tex. The translation was initiated by Lars Eldén on Mon Nov 27 16:19:13 MET 1995