Back to Hans Lundmark's main page

1. Introduction

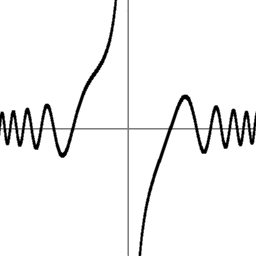
Example. Below are two plots of the function f (z) = sin(z³−1) / z :

• An ordinary real plot y = f (x) from x = −3 to x = +3.
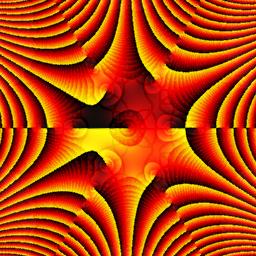
• A "domain coloring" complex plot over a square in the complex plane (lower left corner z = −3−3i, upper right z = +3+3i). Each point z is colored according to the value of f (z).

Virtually all information in the real plot can be read off from just the middle horizontal line z = x+0i in the complex plot (once you learn how to interpret it). But the complex plot also reveals new phenomena that can't be seen in the real plot.

2. My stuff

• Visualizing complex analytic functions using domain coloring.
• Taylor polynomials of the exponential function.
• Elliptic functions.
• Slides in Swedish (pdf) from a talk that I've given a number of times in the course Matematiska utblickar here at Linköping University.

The HTML files are produced with the TtH TeX-to-HTML translator, which uses symbol fonts to render mathematical characters. The versions differ in how the math symbols are encoded. See the TtH manual for details.

You can also get the LaTeX source and a typeset DVI version (without the images).

3. References

Books

There are lots and lots of books about complex analysis. There is one which should be of particular interest for visitors to this site:

• Visual Complex Functions: An Introduction with Phase Portraits by Elias Wegert.
• See also prof. Wegert's paper Phase Plots of Complex Functions: a Journey in Illustration (pdf) from Notices of the AMS, and an article about visualization of complex functions in Frankfurter Allgemeine Zeitung(!) in February 2011, where he was interviewed: Komplexe Zahlen: Das Pünktchen auf dem i (in German, obviously).

Here are a few other books that I can recommend:

• Visual Complex Analysis by Tristan Needham. An amazing book, which uses traditional visualizations methods in a very beautiful way.
• Complex Variables by Mark J. Ablowitz and Athanassios S. Fokas. This book starts from the beginning and works its way up to several interesting topics which are rarely seen in undergraduate textbooks, like Painlevé equations, asymptotic evaluations of integrals, and Riemann–Hilbert problems.
• Complex Analysis: The Geometric Viewpoint by Steven G. Krantz. A nice little book where you can learn more about Picard's theorems, for example.

Internet sources

The first web page I saw on domain coloring was the one by Frank Farris, who also coined the term. There he shows the idea, but his pictures are a little primitive. Other people, including me of course, have tried to make better pictures. Here are some that I am aware of (in no particular order):

• Larry Crone, who in September 2002 informed me that he has been using domain coloring for 15 years already. On his web site you will find not only the standard functions that everybody plots, but also some interesting images of complicated meromorphic functions called "G functions".
• Another early example is the paper "Conformal Image Warping" (PDF file) by Carl Frederick and Erik L. Schwartz, IEEE Computer Graphics and Applications, March 1990.
• MATLAB creator Cleve Moler (in the supplement there is a MATLAB file zviz.m producing very neat pictures).
• George Abdo and Paul Godfrey.
• Jan Hlavacek has a gallery with many interesting images: modular functions, Riemann zeta function, etc.
• G. A. Edgar.
• Bernd Thaller, with a Mathematica package ComplexPlot.m for making color plots of complex functions. Also nice visualizations of examples from Quantum Mechanics.
• John L. Richardson.
• François Labelle. More nice pictures of the Taylor polynomials of e^z, plus the Riemann zeta function and the iteration leading to the Mandelbrot set.
• Platonic tilings of Riemann surfaces by Gerard Westendorp. Color plots of automorphic functions, among lots of other pretty graphics.
• Gallery of plots made with the very impressive Python multi-precision library mpmath written by Fredrik Johansson. Color plots of Airy, Bessel, theta functions, along with the Riemann zeta function and more.
• John E. Davis with plots produced by a script written in his programming language S-Lang.

• Robert Liebo at TU Wien has written a Master's Thesis, Visualization of Complex Function Graphs in Augmented Reality, which is available as a PDF file.
• Architecture student Daniel Piker has some interesting ideas on how to to use of complex mappings to design buildings. See his essay on Rheotomic surfaces, which has lots of nice pictures and animations.
• The conference paper Lifted Domain Coloring (PDF file) by Konstantin Poelke and Konrad Polthier (Freie Universität Berlin) contains plenty of pretty pictures, including colorings of Riemann surfaces instead of just the complex plane.
• Mathematics artist Owen Maresh uses domain coloring too.
• Souichiro Ikebe has a webpage full of amazing graphics illustrating various special functions.
• Winding numbers and domain coloring, a video by the one and only 3Blue1Brown.

• Mathematica nowadays has builtin support for domain coloring; see the documentation for the function ComplexPlot. Earlier suggestions for how to make domain coloring plots with Mathematica can be found in this question and this one on Mathematica Stack Exchange, or this one on Stack Overflow.
• Michael J. Gruber has written with a Python-Fu plugin conformal.py for GIMP, which gives access to Python's powerful features from within GIMP, in particular the special functions module from SciPy.
• Real-Time Zooming Math Engine (rtzme) by Zoltán Kovács is a program for making domain coloring plots, with particular emphasis on speed; it uses the fast zooming algorithm developed for the well-known fractal software XaoS. A binary for SuSE Linux is available, as well as the source code, which Zoltán says should be possible to compile under Windows too.
• Domkol is an HTML5/Javascript/SVG/Canvas/JQuery application by Philip Dorrell which runs in your web browser and displays a domain coloring plot of a cubic polynomial; you can interactively change the location of the zeros. (Works best in the Chrome/Chromium browser.)
• Webpage for making (interactive) phase plots by Jim Fowler and Steve Gubkin.
• Very nice Complex Function Plotter by Samuel J. Li, including support for some special functions like Γ(z) and ζ(z).
• Nico Schlömer's cplot is a Python/numpy library for domain coloring plots.

• Complex Analysis Project at California State University Fullerton has lots of material, both in traditional textbook style and for computer exploration.
• The video Möbius Transformations Revealed by Douglas Arnold and Jonathan Rogness was an unexpected hit on YouTube during the second half of 2007.

4. Technical details

Software used

Most pictures were made on a PC running GNU/Linux, using the GNU Image Manipulation Program (GIMP). For the actual domain coloring stuff, and for the y = f (x) plot above, I used the MathMap GIMP plugin by Mark Probst, slightly hacked by me to allow the elementary functions to take complex arguments. These changes were then incorporated into MathMap v0.12 (a long time ago), and the plugin now also comes with example files for making domaing coloring plots.

Some of the more recent pictures were made with a buggy and ugly Python program that I wrote, since I had problems with MathMap for a while (old versions of MathMap not working with new versions of GIMP). If I can pull myself together some day and tidy up this Python program (not likely to happen very soon) I will make it available here, but right now I'd like to keep it to myself. But you don't need to worry about that, since nowadays MathMap development is active again, so you should be able to use that (or any of the other software packages mentioned above) if you want to make your own plots.

The Julia set was drawn with the Fractal Explorer GIMP plug-in. The formula in the example above was generated by the TeX input for GIMP plug-in written by Dov Grobgeld.

The HTML in the main document "Visualizing complex analytic functions using domain coloring" was generated by Ian Hutchinson's TtH TeX-to-HTML translator. The LaTeX source for that, like the HTML on this start page, was written using Emacs.

(Obsolete) Scheme script for making domain coloring plots

Here is a script that used to work once upon a time, with older versions of GIMP and MathMap. If you want to try it out, good luck, but I can't give any warranties or support.

You need GIMP with the MathMap plug-in installed. Download the Scheme file and put it in the GIMP scripts directory. The next time you start GIMP, a menu entry Script-Fu/MathMap/Domain Coloring should appear in the Xtns menu in the toolbox.

Original version 2000-08-10. Last modified 2024-08-14. Hans Lundmark (hans.lundmark@liu.se)