Shockpeakon solutions of the DP equation

The Degasperis–Procesi (DP) equation is the nonlinear integrable PDE m_t+m_xu+3mu_x = 0, where m = u−u_xx. Like its more famous cousin, the Camassa–Holm shallow water equation m_t+m_xu+2mu_x = 0, it admits a particular type of solutions called peakons (peaked solitons).

Peakons

The n-peakon solution is a superposition of n interacting peak-shaped waves, each with its own time-dependent position x_k(t) and amplitude m_k(t):

u(x,t) = ∑ m_k(t) exp(−|x−x_k(t)|).

GIF animation of a 4-peakon solution of the DP equation

These solutions must be interpreted in a suitable weak sense, since u is not differentiable in the classical sense everywhere (the derivative u_x is a piecewise continuous function, which is undefined at the points x_k where it has jump discontinuities).

(Read more about peakons on another page.)

Shockpeakons

While trying to understand what happens at a "peakon–antipeakon collision" (see below), I found that the DP equation (unlike the Camassa–Holm equation whose solutions must be continuous) also has a class of even weaker solutions that I called shockpeakons, where the wave profile u itself has jump discontinuities (shocks):

u(x,t) = ∑ [m_k(t) − s_k(t) sgn(x−x_k(t))] exp(−|x−x_k(t)|).

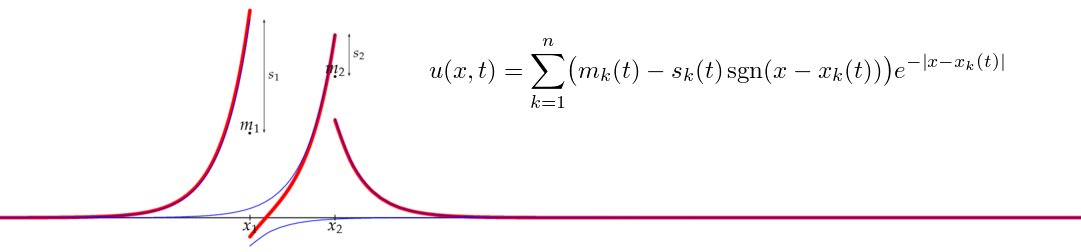
This formula gives a solution of the DP equation provided that the positions x_k, amplitudes m_k and shock strengths s_k satisfy a certain system of 3n ordinary differential equations. (Explicit solution formulas for these ODEs when shocks are present are only known in a few simple special cases, but the system can of course be approximately integrated by numerical methods.)

It's quite unusual to have this kind of (relatively) explicit examples of very weak solutions to such a complicated PDE. Shockpeakons (and ordinary peakons) are useful as test cases when designing numerical methods for the DP equation.

Below is a movie showing a solution of the DP equation where a shockpeakon forms at a collision between a peakon (m₁ > 0) and an antipeakon (m₂ < 0). (There is also a larger version with annotations: 4 MB GIF animation.)

GIF animation of a shockpeakon forming at a peakon-antipeakon collision in the DP equation

In this example, the peakon is a little stronger than the antipeakon, so the resulting shockpeakon moves to the right. (The total momentum m₁ + m₂, in this case a positive number, is conserved throughout the process, and therefore the newborn shockpeakon has positive momentum.)

For the Camassa–Holm equation, the behaviour is different: there the peakon and the antipeakon just pass through each other. Compare the following figures (click on the images for larger versions):

Camassa–Holm peakon-antipeakon collision

Degasperis–Procesi peakon-antipeakon collision

(To be precise: the CH figure shows the so-called conservative solution. There is also a dissipative solution where the peakon–antipeakon pair doesn't reappear after the collision and the lower picture therefore would show just a single peakon, and there are also intermediate cases where the peakon–antipeakon pair reappears although with less energy than it had before the collision.)

Around the same time as I was playing around with explicit solutions and discovered shockpeakons, Giuseppe Maria Coclite and Kenneth Hvistendahl Karlsen released a preprint about discontinuous solutions to the DP equation in general, with focus on questions like existence and wellposedness in certain function spaces. This was very lucky for me, since they knew a lot of things that I didn't!

One thing that I learned from the paper of Coclite and Karlsen was the concept of entropy solution. For weak solutions, the PDE itself may not be enough to determine the solution uniquely. An entropy condition is one kind of additional condition which can be imposed on the solution in order to guarantee uniqueness. The general formulas are a bit technical, so I will not go into that here, but for shockpeakons the situation is simple: they are entropy solutions provided that all s_k are nonnegative, meaning that the jumps in the solution u must go from high on the left to low on the right (as in the pictures and movies).

Even though the DP equation is formally integrable (it has a Lax pair, etc.), the shockpeakon ODEs are still unsolved except in the trivial case n = 1, and a in subcase of a symmetric special case of the case n = 2. The methods used to compute the n-peakon solution (without shocks) don't seem to work when shocks are present, and some quantities that are conserved for nice solutions are not conserved for discontinuous solutions. So, who knows, maybe the DP equation should not be considered integrable when studying discontinuous solutions?

Last modified 2019-12-25. Hans Lundmark (hans.lundmark@liu.se)