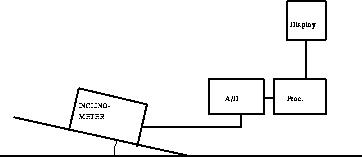
Figure: Instrument för elevationsvinkelmätning
Ett instrument för elevationsvinkelmätning konstruerades för några år sedan av en civilingenjör utexaminerad från LiTH. Instrumentet byggdes enligt följande principschema.
Figure: Instrument för elevationsvinkelmätning
Processorn antas ha flyttalsaritmetik. Inclinometern ger som utdata
en likspänning, som är proportionell mot sinus för vinkeln,
för enkelhets skull antar vi att proportionalitetskonstanten är
lika med 1. Efter A/D-omvandling, som ger ett digitalt sinus-värde
s, beräknar processorn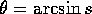 
, som visas på
displayen.
Problemet i det aktuella fallet var att inclinometern inte gav
sinus-funktionen exakt. För att kalibrera instrumentet satte man det
i ett vinkelbord, ställde in ett antal vinklar och mätte upp
utsignalen från inclinometern. Antag att man fick följande
värden. Vinkeln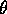 
är given i radianer.
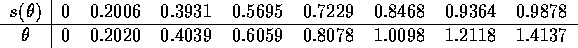
Vi interpolerar nu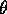 
som funktion av s med ett polynom
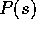, dvs vi bestämmer polynomet P så att 
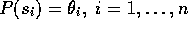. Då kan vi, givet en instrumentspänning s,
direkt beräkna motsvarande vinkel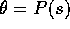 
.
Uppgiften är nu att hitta en lämplig interpolationsmetod, och att implementera denna i processorn. Vi prövar två olika alternativ:
En fördel med denna metod är att vi bestämmer ett enda polynom, som vi använder i hela intervallet. Koden för att evaluera polynomet blir på så sätt mycket enkel.
Vi prövar med att interpolera med ett polynom av grad 7. Resultatet visas i Figur 2.
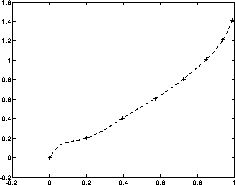
Figure 2: Interpolation med polynom av grad 7. Mätvärdena markeras
med '+' och den interpolerande funktionen utgörs av kurvan.
Vi ser att felet verkar vara stort nära origo. Vi försöker därför att nedbringa felet genom att använda fler mätpunkter, t ex 16, och ett polynom av grad 15. Resultatet ges i Figur 3.
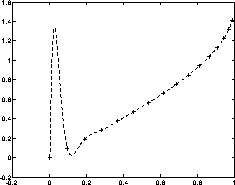
Figure 3: Interpolation med polynom av grad 15.
Vi är tydligen på helt fel väg.
I stället prövar vi att interpolera med en kubisk spline-funktion.
Vi bestämmer alltså en funktion S, som är ett tredje-gradspolynom på
varje intervall, sådan att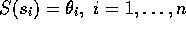 
,
och att första- och andra-derivatan av S är kontinuerliga.
Vi behöver dessutom två randvillkor.
Eftersom vi vet att den interpolerade funktionen är en approximation
till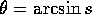 
kan vi använda de ``rätta'' randvillkoren
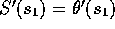och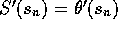 
.
Resultatet visas i Figur 4.
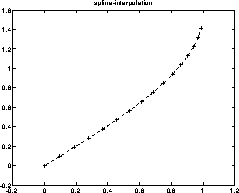
Figure 4: Interpolation med kubisk spline. ``Rätta'' randvillkor.
Interpolation med polynom av högt gradtal fungerar inte i regel, det interpolerande polynomet får kraftiga oscillationer (Runges fenomen, avsnitt 5.2). I det aktuella fallet användes en algoritm baserad på en interpolerande kubisk spline-funktion. Algoritmen implementerades på en mikroprocessor i elevationsvinkelmätaren.
This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds. The command line arguments were:
latex2html -split 0 matinstr.tex. The translation was initiated by Lars Elde'n on Mon Nov 27 16:35:55 MET 1995